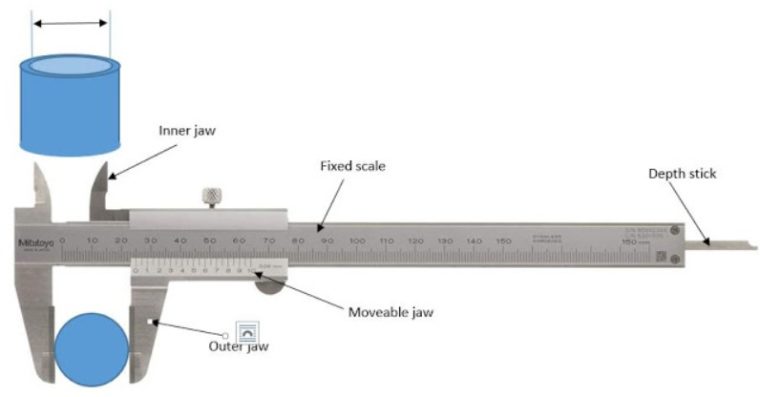
Contoh Soal Jangka Sorong dan Jawabannya

Contoh Soal  IPAS Materi Pembelajaran Jangka Sorong dan Jawabannya

Biar anda lebih paham tentang jangka sorong, di bawah ini sudah kami kumpulkan
beberapa contoh soal Jangka Sorong beserta jawaban dan pembahasannya.
Mari kita simak pembahasannya.
1. Sebuah batu bata diukur ketebalannya menggunakan jangka sorong. Hasil
pengukuran menunjukkan skala seperti pada pada gambar berikut ini :

 

Berapakah tebal batu bata tersebut?

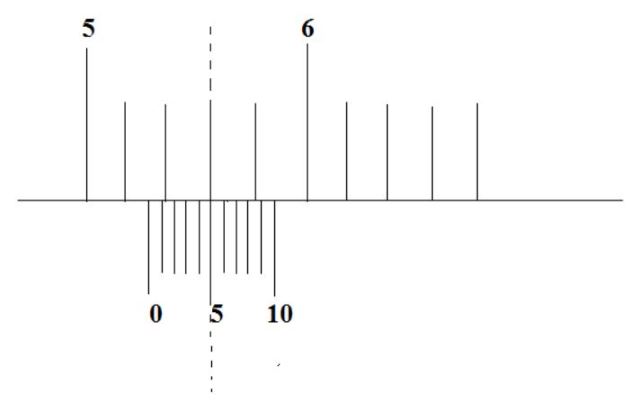
Pembahasan

Skala utama = 5,1cm
Skala vernier= 5 x 0,01 = 0,05cm
Tebal Bata= 5,1 cm + 0,05 cm = 5,15cm
Jadi, tebal batu bata tersebut adalah 5,15cm.

2. Suatu balok kayu diukur menggunakan jangka sorong dengan
hasil pengukuran
seperti gambar di bawah. Berapa tebal balok kayu tersebut ?

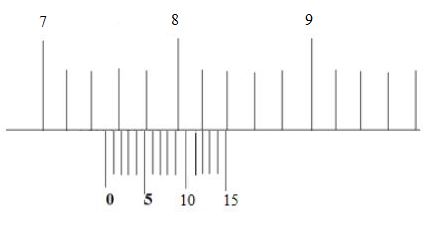
Pembahasan

Skala utama = 7,2cm
Skala vernier= 12 x 0,01 = 0,12cm
Tebal Balok= 7,2 cm + 0,12 cm = 7,32cm
Jadi, tebal balok kayu tersebut adalah 7,32cm.

3. Rudi mengukur diameter sebuah pipa menggunakan jangka
sorong dengan hasil pengukuran sebagai berikut.

Berapakah panjang diameter pipa tersebut?

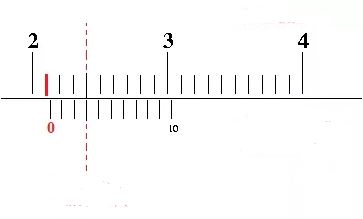
Pembahasan

Skala utama = 4,1cm
Skala vernier= 3 x 0,01 = 0,03cm
Diameter Pipa= 4,1 cm + 0,03 cm = 4,13cm
Jadi, panjang diameter pipa tersebut adalah 4,13cm.

4. Lia membeli 4 buah buku tulis yang sama lalu mengukur ketebalan
empat buku tersebut dengan jangka sorong dengan hasil pengukuran s
ebagai berikut.

Berapakah tebal 1 buah buku tulis tersebut?

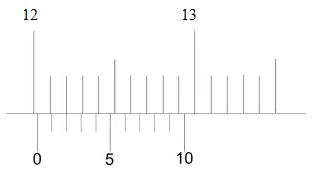
Pembahasan

Skala utama = 12,0cm
Skala vernier = 2 x 0,01 = 0,02cm
Tebal 4 Buku = 12,0cm + 0,02cm = 12,02cm
Tebal 1 Buku = 12,02cm ÷ 4 = 3,005cm
Jadi, tebal 1 buku tulis tersebut adalah 3,005cm.

5. Lisa memiliki sebuah kotak pensil berbentuk balok dengan volume
sebesar 656,25cm³. Dia mengukur lebar kotak pensil tersebut menggunakan
jangka sorong dengan hasil pengukuran sebagai berikut.

Jika diketahui tinggi kotak pensil tersebut adalah 5cm, berapakah
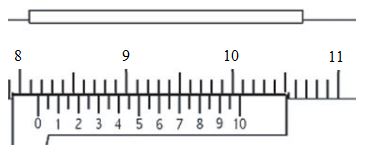
panjang kotak pensil tersebut?

Pembahasan

Rumus volume balok adalah
Volume = panjang × lebar × tinggi
Tinggi kotak pensil tersebut = 5cm
Lebar kotak pensil tersebut adalah:
Skala utama = 8,1cm
Skala vernier = 6,5 x 0,01 = 0,65cm
Lebar kotak pensil = 8,1cm + 0,65cm = 8,75cm
Substitusikan nilai tinggi dan lebar ke rumus volume, maka:
Volume = panjang × lebar × tinggi
656,25cm³ = panjang × 8,75cm × 5cm
656,25cm³ = panjang × 43,75cm²
Panjang = 656,25cm³ ÷ 43,75cm²
Panjang = 15cm
Jadi, panjang kotak pensil tersebut adalah 15cm.

Demikian latihan contoh soal jangka sorong beserta jawaban
dan pembahasannya yang dapat kami sajikan. Semoga
dengan memahami kumpulan soal di atas, anda dapat semakin
lihai dalam menjawab persoalan jangka sorong lainnya.
Sekian dan, selamat belajar.

Angka Penting

Angka Penting

1. Pengertian angka penting

Angka penting adalah semua angka yang diperoleh dari hasil 
pengukuran, meliputi angka pasti dan angka taksiran. Penulisan 
angka penting menunjukkan ketelitian suatu hasil pengukuran.

2. Aturan angka penting

Dalam menulis angka penting, terdapat beberapa aturan yang 
perlu diperhatikan, yaitu sebagai berikut.

1. Semua angka bukan nol merupakan angka penting, 
contohnya 2,34 memiliki tiga angka penting, 65,765 
memiliki lima angka penting.
2. Semua angka nol yang terletak di antara angka bukan 
nol merupakan angka penting, contohnya 3,009 
memiliki empat angka penting, 70,6 memiliki tiga angka 
penting.
3. Angka nol yang terletak di sebelah kanan angka 
bukan nol merupakan angka penting, contohnya 3.000 
memiliki empat angka penting, 1,230 memiliki empat
 angka penting.
4.Angka nol yang terletak di sebelah kiri angka bukan nol, 
baik di kiri maupun di kanan koma bukan termasuk angka 
penting, contohnya 0,1 memiliki satu angka penting, 0,005 
memiliki 1 angka penting, 0,0567 memiliki tiga angka penting.
Semua angka sebelum faktor pengali pada notasi ilmiah 
merupakan angka penting.

3. Operasi angka penting

a. Operasi penjumlahan dan pengurangan

Tidak ada aturan khusus pada operasi penjumlahan dan 
pengurangan, hanya saja pembulatan untuk bilangan 
desimal mengikuti angka taksiran paling sedikit. 
Contohnya adalah sebagai berikut. 

Untuk pembulatan, jika angka terakhir lebih besar dari lima, 
bulatkan ke atas. Jika angka terakhir lebih kecil dari lima, 
bulatkan ke bawah. Jika tepat lima, lihat angka sebelumnya, 
misal angka sebelumnya ganjil bulatkan ke atas dan sebaliknya. 
Contoh:

b. Operasi perkalian dan pembagian

Jika menggunakan aturan angka penting, hasil perkalian antara 
dua bilangan atau lebih menghasilkan bilangan yang jumlah 
angka pentingnya sama dengan angka penting paling sedikit. 
Contohnya sebagai berikut.

A. Pembulatan

Aturan dalam pembulatan angka penting adalah sebagai berikut.

1. Angka lebih dari 5 dibulatkan ke atas dan angka kurang 
2. dari 5 dihilangkan.
   Contoh:
   a. 246,86 dibulatkan menjadi 246,9
   b. 416,64 dibulatkan menjadi 416,6
3. Apabila tepat angka 5, dibulatkan ke atas jika angka 
4. sebelumnya angka ganjil, dan dihilangkan jika angka 
5. sebelumnya angka genap.
   Contoh:
   a. 246,65 dibulatkan menjadi 246,6
   b. 326,55 dibulatkan menjadi 326,6.

B. Penjumlahan & Pengurangan

Operasi pengurangan & penjumlahan angka penting mengikuti
aturan sebagai berikut: Penulisan hasil operasi penjumlahan &
pengurangan hanya boleh memiliki satu angka ragu-ragu /
taksiran / angka tak pasti.
Contohnya : 12 cm (2 adalah angka tak pasti) + 2,85 cm (5
angka tak pasti) = 14,85 ( 4 dan 5 adalah Angka tak pasti)
kemudian, dibulatkan agar hanya ada 1 angka tak pasti,
menjadi 15.

C. Perkalian & Pembagian

Operasi perkalian dan pembagian mengikuti aturan sebagai
berikut.

Jumlah angka penting pada hasil akhir harus mengikuti
jumlah AP yang paling sedikit.
Untuk perkalian dan pembagian angka penting dengan
angka eksak, hasil akhir mengikuti jumlah AP tersebut.

Contohnya : 125 cm (3 AP) dikalikan 10 (1 AP) = 1250,
karena masih ada 3 AP, maka harus dijadikan 1 AP saja.
Sehingga hasilnya menjadi 1000 (1 angka penting).

Contoh Soal & Pembahasan

Berikut contoh soal angka penting yang melibatkan perhitungan.

1. Berikut bilangan yang hanya terdiri dari dua angka penting adalah… .
   1. 0,00021
   2. 120,01
   3. 13,00
   4. 3,0
   5. 10

Jawaban: A dan D
Perhatikan aturan significant figures nomer 4 dan 5.
Aturan ke 4
Angka nol di depan angka bukan nol adalah bukan AP.
Sehingga 0,00021 hanya terdiri dari dua AP.
Aturan ke 5
Angka nol di belakang tanda desimal dan mengikuti 

angka bukan nol adalah AP.
Sehingga bilangan 3,0 teridiri dari 2 angka penting.

2. Berikut bilangan yang hanya terdiri dari 4 angka penting adalah….
   1. 0,00021
   2. 120,01
   3. 13,00
   4. 3,0
   5. 10

Jawaban: D
Perhatikan aturan significant figures nomer 5. 

Angka nol di belakang tanda desimal dan 

mengikuti angka bukan nol adalah AP. Sehingga 

bilangan 13,00 teridiri dari 4 AP.

3. Panjang sisi persegi panjang adalah 12 m dan 
4. 5,55 m. Tentukan;
   1. keliling dan
   2.  luas persegi panjang tersebut!

Jawaban:
(a) Keliling persegi panjang
K=2(p+l)=35,10

Angka 5 dan 0 adalah angka ragu-ragu, sehingga 

hasilnya harus dibulatkan menjadi 35 agar hanya 

mengandung satu angka ragu-ragu saja.

(b) Luas persegi panjang

L=p×l=66.60

Panjang persegi dinyatakan oleh dua AP dan lebar 

dinyatakan oleh tiga AP. Sehingga luasnya hanya 

boleh mengandung dua angka penting. 

Jadi luasnya adalah 67 m2.

 

Contoh Soal mikrometer sekrup

Contoh Soal 1

Sebuah mikrometer sekrup digunakan untuk mengukur diameter bola kecil dengan hasil sebagai berikut.

Berdasarkan gambar di atas, berapakah diameter bola kecilnya?
Pembahasan:
Diketahui:

Ditanya: diameter bola kecil =…?
Penyelesaian:
Berdasarkan gambar dihasilkan:
Skala utama = 8 mm
Skala nonius = 16 x 0,01 = 0,16 mm
Hasil Pembacaan Alat = skala utama + skala nonius
  = 8 mm + 0,16 mm
  = 8,16 mm
Jadi, diameter bola kecilnya adalah 8,16 mm.

Contoh Soal 2

Arda mengukur tebal pelat baja menggunakan mikrometer sekrup dan diperoleh gambar berikut.

Berapakah ketebalan pelat baja Arda?
Pembahasan:
Diketahui:

Ditanya: ketebalan pelat baja Arda =…?
Penyelesaian:
Berdasarkan gambar dihasilkan:
Skala utama = 2,5 mm
Skala nonius = 22 x 0,01 = 0,22 mm
Hasil Pembacaan Alat = skala utama + skala nonius
  = 2,5 mm + 0,22 mm
  = 2,72 mm
Jadi, ketebalan pelat baja Arda adalah 2,72 mm.

Mikrometer Sekrup

Mikrometer Sekrup
 Mikrometer sekrup adalah alat pengukuran yang terdiri
dari sekrup terkalibrasi dan memiliki tingkat kepresisian
0.01 mm (10^-5 m). Alat ini ditemukan pertama kali oleh
Willaim Gascoigne pada abad ke-17 karena dibutuhkan
alat yang lebih presisi dari jangka sorong. Penggunaan
pertamanya adalah untuk mengukur jarak sudut antar
bintang-bintang dan ukuran benda-benda luar angkasa dari teleskop.

Bagian-Bagian Mikrometer Sekrup

  

 

Cara Menggunakan Mikrometer Sekrup

Prinsip kerja mikrometer sekrup adalah menggunakan suatu
sekrup untuk memperbesar jarak yang terlalu kecil untuk
diukur secara langsung menjadi putaran suatu sekrup lain
yang lebih besar dan dapat dilihat skalanya.
Cara menggunakan mikrometer sekrup adalah:

1. Objek yang ingin diukur diletakkan menempel dengan 
2. bagian poros tetap.
3. Setelah itu, bagian thimble diputar hingga objek terjepit 
4. oleh poros tetap dan poros geser.
5. Bagian ratchet dapat diputar untuk menghasilkan perhitungan 
6. yang lebih presisi dengan menggerakkan poros geser s
7. ecara perlahan.
8. Setelah yakin bahwa objek benar-benar terjepit diantara
9. kedua poros, hasil pengukuran dapat dibaca di skala utama 
10. dan skala nonius.

Cara Membaca Mikrometer Sekrup

Pembacaan mikrometer sekrup dilakukan pada dua bagian, yaitu
di skala utama dan di skala nonius atau Vernier. Skala utama
dapat dibaca di bagian sleeve dan skala nonius dapat dibaca
 di bagian thimble.

Mikrometer Sekrup

Sumber gambar: miniphysics.com

Pada contoh pengukuran di atas, cara membaca mikrometer sekrup
tersebut adalah:

• Untuk skala utama, dapat dilihat bahwa posisi thimble telah 
• melewati angka “5” di bagian atas, dan pada bagian bawah 
• garis horizontal telah melewati 1 strip. 0.5mm. Artinya, pada 
• bagian ini didapat hasil pengukuran 5 + 0.5 mm = 5.5 mm. 

Pengukuran juga dapat dilakukan dengan prinsip bahwa setiap

1 strip menandakan jarak 0.5mm. Dikarenakan terlewat                                                                

5 strip di atas garis horizontal dan 6 strip di bawah garis   

horizontal, maka total jarak adalah (5+6) x 0.5mm = 5.5mm
Pada bagian kedua, terlihat garis horizontal di skala utama 

berhimpit dengan angka 28 di skala nonius. Artinya, pada 

skala nonius didapatkan tambahan panjang 0.28mm
Maka, hasil akhir pengukuran mikrometer sekrup pada 

contoh ini adalah 5.5 + 0.28 = 5.78mm. Hasil ini memiliki 

ketelitian sebesar 0.01 mm.

Fungsi Mikrometer Sekrup

Mikrometer sekrup pada umumnya digunakan untuk mengukur
diameter atau ketebalan suatu benda yang ukurannya kecil. Seperti
dijelaskan sebelumnya, alat ini memiliki kepresisian 10x lipat dari
 jangka sorong sehingga dapat mengukur benda yang lebih kecil
tepatnya pada ketelitian 0,01 mm.
Penggunaan alat ini untuk mengukur panjang benda kurang umum
digunakan, karena umumnya panjang benda masih dapat diukur
dengan baik di tingkat kepresisian 1 mm dan 0,1 mm, dimana
masing-masing tingkat kepresisian dimiliki oleh penggaris
dan jangka sorong.

Jangka Sorong

Jangka Sorong

Pengertian Jangka Sorong Jangka sorong adalah alat yang bisa mengukur panjang dan ketebalan suatu benda dengan tingkat akurasi dan presisi yang sangat baik yaitu sekitar +- 0.05 mm. Jangka sorong biasanya dipakai oleh para enginer buat mengukur diameter benda atau lubang pipa. Gak cuma itu, jangka sorong juga bisa mengukur kedalaman atau ketinggian sebuah lubang kecil.Pada jangka sorong juga ada 2 buah skala yang dipakai buat membaca hasil pengukuran. Pertama yaitu skala utama yang memakai satuan centimeter dan milimeter pada bagian bawah dan satuan inch pada bagian atas. Kedua adalah skala nonius atau  vernier. Fungsi Jangka Sorong   Dibawah ini ada beberapa fungsi dari sebuah jangka sorong atau vernier caloper dalam pengukuran suatu benda, diantaranya yaitu: Buat mengukur tinggi suatu benda yang bertingkat. Buat mengukur ketebalan suatu benda dan benda yang  diukur bisa berbentuk  bulat, bujur sangkar, balok, persegi, kubus dan lainnya. Buat mengukur outer ring atau bagian luar benda. Buat mengukur inner ring atau bagian dalam suatu benda. Buat mengukur kedalaman suatu benda.